RLIBM: Rutgers Architecture and Programming Languages Lab's Correctly Rounded Libm

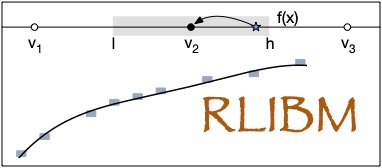
The RLIBM project is building a collection of correctly rounded elementary functions for multiple representations ( e.g., 32-bit float, posits, bfloat16, tensorfloat32) for multiple rounding modes. This project makes a case for approximating the correctly rounded result of an elementary function rather than the real value of an elementary function. When we approximate the correctly rounded result, there is an interval of real values around the correctly rounded result such that producing a real value in this interval rounds to the correct result. This interval is the freedom that the polynomial approximation has for an input, which is larger than the freedom with prior approaches (i.e., mini-max approaches). Hence, the RLIBM approach has more margin to generate correct, yet, efficient polynomials.

Using these intervals, we structure the problem of generating polynomial approximations that produce correctly rounded results for all inputs as a linear programming problem. We have developed correctly rounded implementations of elementary functions for multiple representations: 32-bit floating point, 32-bit posits, 16-bit posits, bfloat16, and tensorfloat32.

We are collaborating with the community in the effort to make correct rounding mandatory in the next versions of the floating point standard. The CORE-MATH project and the LLVM's math library also provide correctly rounded functions. See also the argument for correct rounding by Brisebarre, Hanrot, Muller, and Zimmermann.

Participants

• Santosh Nagarakatte (PI)
• Mridul Aanjaneya (Co-PI)
• Sehyeok Park (current Rutgers CS Ph.D. student)
• Jay P. Lim (former Rutgers CS Ph.D. student, graduated October 2021)

Prior Collaborators and Participants

• Justin Kim (Rutgers CS Undergraduate student, 2023-2024)
• John Gustafson

Transition to Practice

• LLVM's log2f uses RLIBM's polynomials. Discussion about the polynomials and performance during the review process. See here.
• LLVM's logf uses RLIBM's polynomials. The review process had interesting discussion about the polynomials and performance. See here.
• LLVM's log10f uses polynomials inspired from the RLIBM approach.
• LLVM's exp2f performance significantly improved with range reduction from the RLIBM approach.
• LLVM's expf performance significantly improved with range reduction from the RLIBM approach.

Blog posts

• ACM SIGPLAN blog post on our POPL 2022 Distinguished Award paper: "One Polynomial Approximation to Produce Correctly Rounded Results for Multiple Representations and Rounding Modes"
• ACM SIGPLAN blog post on our PLDI 2021 Distinguished Award paper: "High Performance Correctly Rounded Math Libraries for 32-bit Representations"

Code

• Latest functions from the RLIBM project
• RLIBM-PROG: Progressive Polynomial Approximations for Fast Correctly Rounded Math Libraries
• RLIBM-ALL: Correctly Rounded Elementary Functions for Multiple Rounding Modes and Multiple Representations
• RLIBM-32 for 32-bit Representations
• RLIBM for 16-bit Representations

Talks

• Santosh Nagarakatte's talk at the 2022 Papers We Love Conference summarizing the results from the RLIBM project.
• Mridul Aanjaneya's PLDI 2022 Conference talk.
• Santosh Nagarakatte's Keynote talk at the 2022 Conference on Next Generation Arithmetic and NJPLSS.
• Santosh Nagarakatte's talk at FPTalks 2022.
• Jay Lim's POPL 2022 talk
• Jay Lim's PLDI 2021 extended talk, PLDI 2021 short talk
• Jay Lim's POPL 2021 extended talk POPL 2021 short talk
• Jay Lim's FPTalks 2021 talk
• Jay Lim's FPTalks 2020 talk
• Santosh Nagarakatte's talk at the University of Wisconsin Madison, MadPL Seminar Series, 2020

Publications

• Maximum Consensus Floating Point Solutions for Infeasible Low-Dimensional Linear Programs with Convex Hull as the Intermediate Representation. [pdf]
  Mridul Aanjaneya and Santosh Nagarakatte
  Proceedings of the ACM Programming Languages (PACMPL), Programming Language Design and Implementation (PLDI-2024) issue, Copenhagen, Denmark, June 24-28, 2024. 26 pages.
  Acceptance rate: 28% (89 out of 316 submissions)
  
  
• Fast Polynomial Evaluation for Correctly Rounded Elementary Functions using the RLIBM Approach. [preprint]
  Mridul Aanjaneya and Santosh Nagarakatte
  Proceedings of the IEEE/ACM International Symposium on Code Generation and Optimization (CGO-2023), Montreal, Canada, Feb 25- March 1st, 2023.
  Acceptance rate: 39% (20 out of 51 submissions)
  
  
• Progressive Polynomial Approximations for Fast Correctly Rounded Math Libraries [preprint]
  Mridul Aanjaneya, Jay P. Lim, and Santosh Nagarakatte
  Proceedings of the 2022 ACM SIGPLAN Conference on Programming Langauge Design and Implementation (PLDI-2022), San Diego, USA, June, 2022.
  Acceptance rate: 21% (68 out of 326 submissions)
  
  
• One Polynomial Approximation to Produce Correctly Rounded Results of an Elementary Function for Multiple Representations and Rounding Modes [preprint]
  Jay Lim and Santosh Nagarakatte
  Proceedings of the 49th ACM SIGPLAN Symposium on Principles of Programming Languages (POPL-2022), Philadelphia, USA, January 16-22, 2022.
  Acceptance rate: 23% (65 out of 286 submissions)
  ACM SIGPLAN POPL 2022 Distinguished Paper Award
  
  
• RLIBM-PROG: Progressive Polynomial Approximations for Fast Correctly Rounded Math Libraries [pdf]
  Mridul Aanjaneya and Jay P Lim and Santosh Nagarakatte
  Department of Computer Science, Rutgers University, Technical Report DCS-TR-758, November 2021
  
  
• Novel Polynomial Approximation Methods for Generating Correctly Rounded Elementary Functions [pdf]
  Jay P Lim's PhD dissertation supervised by Santosh Nagarakatte
  Department of Computer Science, Rutgers University October 2021
  2022 ACM SIGPLAN John C Reynolds Outstanding Dissertation Award
  
  
• RLIBM-ALL: A Novel Polynomial Approximation Method to Produce Correctly Rounded Results for Multiple Representations and Rounding Modes [pdf]
  Jay P Lim and Santosh Nagarakatte
  Department of Computer Science, Rutgers University, Technical Report DCS-TR-757, August 2021
  
  
• High Performance Correctly Rounded Math Libraries for 32-bit Floating Point Representations [preprint]
  Jay P Lim and Santosh Nagarakatte
  Proceedings of the 2021 ACM SIGPLAN Conference on Programming Language Design and Implementation (PLDI-2021), June 20-25, 2021.
  Acceptance rate: 27% (87 out of 320 submissions)
  ACM SIGPLAN PLDI 2021 Distinguished Paper Award
  
  
• RLIBM-32: High Performance Correctly Rounded Math Libraries for 32-bit Floating Point Representations [pdf]
  Jay P Lim and Santosh Nagarakatte
  Department of Computer Science, Rutgers University, Technical Report DCS-TR-754, April 2021
  Extended version of our PLDI 2021 paper.
   
• An Approach to Generate Correctly Rounded Math Libraries for New Floating Point Variants [preprint]
  Jay P Lim, Mridul Aanjaneya, John Gustafson, and Santosh Nagarakatte
  Proceedings of the 2021 ACM SIGPLAN Symposium on Principles of Programming Languages (POPL-2021), Jan 17-22, 2021.
  Acceptance Rate: 23% (61 out of 258 submissions).
  
  
• A Novel Approach to Generate Correctly Rounded Math Libraries for New Floating Point Representations [pdf]
  Jay P Lim, Mridul Aanjaneya, John Gustafson, and Santosh Nagarakatte
  Department of Computer Science, Rutgers University, Technical Report DCS-TR-753, July 2020
   

Funding:

• Intel Corporation Research Gift, $62,000, "A Case for Correctly Rounded Math Libraries with the RLIBM project" , 2023-2024.
• NSF CORE Program-SHF, $540,000, "Efficient, Deterministic and Formally Certified Methods for Solving Low-dimensional Linear Programs with Floating-point Precision", 2023.
• Intel Corporation Research Gift, $62,000, "A Case for Correctly Rounded Math Libraries with the RLIBM Approach", 2022-2023.
• NSF CORE Program-SHF, $499,979, "Techniques for Generating Correctly Rounded Math Libraries", 2021.
• NSF CORE Program-SHF, $500,000, "Formalisms, Implementations, and Verification Procedures for Alternatives to Floating Point", 2019-2022.