Cryptography is the practice of secure communication in the presence of third parties. It involves techniques for secure communication, data protection, and identity verification. In this section, we will discuss the evolution of cryptography, covering substitution and transposition ciphers, and algorithms developed for computers. We will later look at the use of cryptography for key distribution, authentication, integrity, and non-repudiation.

The word “cryptography” comes from the Greek roots kryptos for “hidden” and graphia for “writing”, and is defined as “a secret manner of writing.” Cryptanalysis, on the other hand, is the art of undoing what cryptography does, and is defined as “the analysis and decryption of encrypted information without prior knowledge of the keys”. Cryptology is the term for the overall art and science that covers cryptography and cryptanalysis.

Cryptography != Security

Cryptography is not always necessary to build a secure system, it is just a technology that may be part of a secure system. It is a component, and just using encryption does not necessarily make a system secure.

Cryptography: what is it good for?

For well over 2,000 years, cryptography was mostly used for providing confidentiality, allowing us to hide the contents of a message so others cannot read it. However, it is also useful for authentication, allowing us to determine the origin of a message and thus verify the identity of users or services. Cryptography can also provide integrity services, allowing us to detect if a message has been modified by someone else after it has been created. Finally, cryptography enables us to provide non-repudiation, where a sender will not be able to falsely deny sending a message.

Basic Terms in Cryptography

Plaintext: The original message, sometimes called clear text. It can refer to any content.

Encryption: The process of converting plaintext into an unreadable format using a cryptographic algorithm and a key.

Ciphertext: The result of encryption, an unreadable format of the original message.

Decryption: The process of converting ciphertext back into its original plaintext format using a cryptographic algorithm and a key.

Cipher: The cryptographic algorithm used for encryption and decryption.

Key: A piece of information used by the cipher to encrypt and decrypt data.

Secret algorithms

In the history of secure communications, the use of secret algorithms for ciphers has a long-standing history and remains a popular choice in certain contexts. The essence of this approach is to keep the cipher’s mechanics a closely guarded secret, accessible only to a select, trusted group. The main advantage? Simply possessing the cipher allows one to encrypt and decrypt data effectively.

However, there are significant drawbacks to this method. For starters, it hinges on the assumption of unwavering loyalty from those in the know. Consider the scenario where someone, perhaps a disgruntled employee, leaves an organization with knowledge of the cipher. In such cases, the cipher’s security is immediately compromised, forcing the organization to start from scratch with a new cipher.

Another major risk is the potential theft and reverse engineering of the cipher. If it ends up in the wrong hands and its workings are deciphered, the security it was supposed to provide vanishes.

Assessing the robustness of a secret algorithm also poses a challenge. Bruce Schneier, a respected figure in cryptography, once remarked that it’s relatively easy to create an encryption algorithm that even its creator can’t break. However, this doesn’t necessarily translate to a secure algorithm. Limited testing, like asking friends to attempt decryption or offering monetary rewards for breaking the cipher, is insufficient to prove its effectiveness.

In cryptography, the preference often leans towards tried-and-tested algorithms rather than the newest innovations. The field values algorithms that have been rigorously examined and validated by a wide array of experts over an extended period.

A review of historical instances where secret algorithms were broken can be quite revealing. Notable examples include the compromised encryption in DVDs, HD DVDs, and Blu-rays, the RC4 encryption algorithm, all the encryption algorithms used in digital cellular phones, and the FireWire protocol—a secure device protocol similar to USB, developed in the 1990s by companies like Apple, Panasonic, and Sony. Even the famed Enigma cipher machine from World War II, along with many other wartime and Cold War era ciphers, eventually succumbed to decryption. These examples, developed by skilled teams and subjected to thorough reviews, nevertheless had vulnerabilities. This history suggests that a small team of developers, however talented, would face considerable challenges in creating a more secure cipher.

Shared algorithms and secret keys

If we can’t count on secret algorithms to keep our digital secrets, what can we use? The answer lies in something called a secret key.

Let’s break it down with something familiar: a tumbler lock, like the one you might have on your front door. Inside this lock, there’s a setup with two cylinders, one inside the other. The inner one can’t turn because it’s blocked by some pins. These pins are spring-loaded and split into two parts.

When you put the right key into the lock, each of these split pins lifts up to just the right height. This aligns the split exactly at the end of the inner cylinder. Once they’re lined up, the cylinder can turn, and the lock opens.

Even though we can learn all about how the lock works, the real secret isn’t in the lock itself. It’s in the shape of the key. This is a great way to think about computer security too. The algorithm used to encrypt and decrypt data (like the lock) can be known to many, but the security really comes from the secret key. As long as the key stays secret, your data stays safe.

So, even if people know how the security system works, without the secret key, they can’t access the data it’s protecting. Moreover, we can count on many people studying the mechanism of the lock to discover and disclose all of its weaknesses. This allows us to make an educated decision about whether we can trust it for the level of protection we need. It gives us information to decide whether to spend $200 on a Medeco deadbolt or buy a $17 Kwikset model.

Kerckhoffs’s Principle

A core guiding principle in computer security that has stood the test of time, tracing its roots back to the 19th century. It’s known as Kerckhoffs’s Principle, named after August Kerckhoffs, a Dutch linguist and cryptographer who fundamentally changed our approach to thinking about how we secure information.

In 1883, Kerckhoffs proposed a radical idea: “A cryptosystem should be secure even if everything about the system, except the key, is public knowledge.” This concept, initially aimed at military cryptography, has become a guiding principle in modern cybersecurity.

Kerckhoffs’s Principle argues that the strength of a security system lies not in the obscurity of its algorithms but in the secrecy of its key. It’s a simple yet profound shift in thinking: security through obscurity is a fragile defense. In contrast, a well-guarded key in a known system can be remarkably robust.

Imagine a digital vault whose design is open to the world. According to Kerckhoffs, as long as the key (or combination) to this vault remains hidden, the contents are safe. This principle has profound implications in an era where transparency and openness in software development are increasingly valued.

This principle underscores a critical aspect of design strategy: focus on securing the key rather than cloaking the algorithm.

Kerckhoffs’s Principle also reflects a broader theme in digital security: Do not put your trust in the complexity of your cryptographic methods, but in the strength and secrecy of your keys.

Properties of a Good Cryptosystem

A well-designed cryptosystem exhibits several key properties to ensure robust security. Here are the three primary properties:

Indistinguishability from Random Values

The ciphertext, or the encrypted message, should appear completely random. There shouldn’t be any clues in the ciphertext that might hint at the original message or the key that was used to encrypt it. This randomness ensures that the ciphertext doesn’t give away any secrets.

Resistance to Decryption without the Key

It should be impossible to revert the ciphertext back to plaintext, or the original message, without the correct key. This means that even if an attacker has access to multiple plaintext-ciphertext pairs (P, C), or can generate a large amount of ciphertext from chosen plaintext, they still can’t decrypt the message without the key. The only method left would be to try every possible key, which leads to the next point.

Large Key Space

The keys used in the cryptosystem should be large enough to make brute-force attacks – trying every possible key – infeasible. This should hold true even considering the advancements in computing power we anticipate in the next 20 years.

In addition to these core properties, there are several other desirable characteristics in a good cryptosystem:

Key-Centric Secrecy (Kerckhoffs’s Principle): The security of the system should reside in the secrecy of the key, not in the secrecy of the algorithm. The algorithm is often public knowledge, but the key must be kept private.

Efficiency in Encryption and Decryption: The process of encrypting and decrypting data should be fast. This encourages the widespread use of secure cryptography, as it won’t significantly slow down data access.

Simplicity and Versatility: Keys and algorithms should be straightforward and able to operate on any data. Complex algorithms are more prone to implementation errors, and restrictions on keys or data types can undermine security.

Equal Ciphertext and Plaintext Size: Ideally, the size of the ciphertext should be the same as the plaintext to avoid reducing effective bandwidth. While a bit of extra data is sometimes necessary, it should be minimal and not proportional to the length of the plaintext.

Well-tested Algorithms: A trustworthy cryptosystem is one that has undergone rigorous scrutiny over many years by numerous experts. Reliability comes from extensive analysis, not from being the latest innovation on the market.

Understanding these properties helps in the evaluation and development of cryptosystems.

Symmetric key ciphers

In this part, we will look at symmetric key ciphers. To encrypt a message, we provide the message and an extra parameter: the key. To decrypt the message, we apply the decryption algorithm, giving it the ciphertext and the same secret key.

We will start off by examining some classic cryptosystems. These predate computers.

Substitution ciphers

We begin with substitution ciphers, a fundamental and historical approach to encryption. In substitution ciphers, each character in the plaintext (the original message) is replaced by a corresponding character in the ciphertext (the encoded message).

Historically, ciphers primarily served military communication needs. Due to the inherent need for secrecy in these applications, documentation and public dissemination of these methods were uncommon. The guiding principle was straightforward: maintaining secrecy often meant keeping the cipher’s existence and methodology under wraps. Most of the history of cryptography is lost to us.

Furthermore, practicality was key in the design and use of these ciphers. They needed to be simple enough to be written and transmitted without requiring specialized tools or extensive training. This ease of use in both encryption (coding the message) and decryption (decoding the message) was essential, especially in scenarios where messages had to be encoded and decoded swiftly and efficiently on the battlefield.

One of the earliest recorded instances of cryptography can be traced back to ancient Egypt, around 1900 BC. In an inscription found in the tomb of a nobleman named Khnumhotep II, some of the hieroglyphic symbols were written in a non-standard form. This is believed to be an early attempt at encryption but it’s not clear what the goal of this was.

Similarly, ancient Mesopotamia showed evidence of cryptography in cuneiform inscriptions. Here, clay tablets were found with encrypted recipes for pottery glazes. This form of cryptography was possibly used to protect trade secrets rather than for military purposes. The use of cryptography in these contexts demonstrates an early understanding of the value of secret information, whether for economic, personal, or possibly political reasons.

Atbash: An Ancient Hebrew Cipher

The Atbash cipher stands as one of the earliest known ciphers, with its origins tracing back approximately 2600 years in Hebrew history. This cipher is a classic example of a simple yet effective method of encryption.

To utilize the Atbash cipher, one begins by writing out the alphabet in its standard order. Directly beneath, the alphabet is then written out again, but in reverse order. This reversed sequence forms the substitution alphabet.

The process of encoding a message involves substituting each character of the plaintext with the corresponding character from the substitution alphabet. For example, in the Atbash cipher:

• The letter ‘M’ is replaced with ‘N’
• ‘Y’ becomes ‘B’
• ‘C’ transforms to ‘X’

and this pattern continues for each letter in the message. Consider the phrase “my cat has fleas.” When encoded using the Atbash cipher and ignoring spaces, each character in this phrase is substituted according to the pattern outlined above.

The Atbash cipher is an early example of a ‘secret algorithm’ where the mere knowledge of the algorithm’s process is sufficient to both encrypt and decrypt messages. Despite its simplicity, this cipher provides a foundational understanding of basic cryptographic principles.

Caesar Cipher: The Key-Based Ancient Cipher

The Caesar cipher, dating back to the era of Julius Caesar in Rome, is perhaps the first known cipher that utilized a key. It also represents the earliest documented use of cryptography in a military context (even though cryptography was likely used in the military long before that). This cipher is a type of substitution cipher, specifically called a shift cipher.

In the Caesar cipher, a substitution alphabet is created by shifting each letter by a set number of positions, known as the shift value. This shift value, denoted as ‘N’, acts as the key needed to decrypt a message.

How the Caesar Cipher Works

To illustrate, let’s take a look at an example. First, write down the standard alphabet. Below it, write the substitution alphabet. This substitution alphabet is then shifted by a certain number of places - in this example, we’ll use a shift of 6 places.

When encrypting a phrase like “my cat has fleas,” each letter is replaced by the corresponding character in the shifted substitution alphabet. So, ‘M’ is substituted with ‘G’, ‘Y’ becomes ‘S’, ‘C’ changes to ‘W’, ‘A’ turns into ‘U’, ‘T’ shifts to ‘N’, and this pattern is followed for the entire message.

Decryption and Vulnerability

The resulting ciphertext is a jumbled, seemingly unreadable text. To decrypt this message, the only piece of information needed is the shift value. However, the simplicity of the Caesar cipher also makes it quite vulnerable. With a standard 26-letter alphabet, there are only 25 possible shift values (excluding a shift of 0, which would leave the text unchanged).

This limited range of possible shifts means that trying all 25 combinations to crack the code wouldn’t take much time, making the Caesar cipher relatively easy to decipher for someone who knows the technique.

Monoalphabetic Substitution Cipher

The Caesar cipher is actually a specific type of a broader category known as the monoalphabetic substitution cipher. This category is referred to as “monoalphabetic” because it uses the same single (or ‘mono’) substitution alphabet throughout the entire message. The Caesar cipher is a unique case within this category, called a shift cipher, because it involves keeping the substitution alphabet in its original order and simply shifting its position.

In a general monoalphabetic substitution cipher, however, the letters can be scrambled in any order. While this offers a higher level of complexity and security compared to the Caesar cipher, it also introduces practical challenges. Both the sender and receiver need to have an identical copy of the substitution alphabet. Unlike the Caesar cipher’s simple shift, these scrambled substitution alphabets are often too complex to easily memorize.

The potential for security in a general monoalphabetic cipher is immense, primarily due to the sheer number of possible permutations. The 26 letters of the alphabet can be rearranged in 26! ways. To put that in perspective, there are approximately 4x10²⁶ possible permutations. If you were to try a billion permutations per second, it would take about 1.3x10¹⁶ years to go through them all – that’s 13 quadrillion years!

Despite this vast number, many permutations might retain some of the same letter mappings as the original alphabet. However, the number of variations remains staggeringly large, making the general monoalphabetic substitution cipher significantly more secure than its simpler cousin, the Caesar cipher.

Frequency analysis

The number of permutations of the alphabet in a substitution cipher is huge. However, that doesn’t mean we need to try every permutation to decode a message. If we know the language we’re decoding, we can apply a technique called frequency analysis.

Letters don’t appear with the same frequencies in natural languages. For instance, in European languages, you see the letters A and E appear much more frequently in text than X and Z.

The letter frequency distribution is relatively consistent across multiple types of texts if you sample enough text. For example, I compared the complete works of Shakespeare against Herman Melville’s Moby Dick and the frequencies were incredibly similar. If you look at the Letter Frequency article on Wikipedia, you can see letter frequencies for 15 different languages. The letter E appears about 12% of the time, O appears between 7 and 8% of the time and X only 0.1%.

The fact that letters appear with different frequencies leads to a cryptanalytic technique called frequency analysis.

If we examine an encrypted message where 12% of the characters are the letter “X” and we know a substitution cipher was used, that enables us to guess that the “X” is likely to be an “E” in the decrypted version.

Similarly, if we see “E” appear only 1% of the time, then we can guess that it’s most likely a “V” or a “K” when decrypted. We might not be exactly sure of what character to use but we can dramatically cut our search space down to 2 or 3 letters.

To refine our guesses, we can also look at adjacent characters. Groups of two letters are called digrams. In English, digrams like “TH” and “HE” occur about 3% of the time. “IN” and “ER” occur about 2% of the time. For example, if we’re not sure if a character maps to an “S” or “H” because they both occur about 6% of the time in the text but we see it often follows a character that we decided decrypts to a “T”," we can assign a much higher probability to it being an “H” because the “TH” digram is much more common than “TS.” If needed, we can look at common trigrams to further refine our guesses.

Entropy

Claude Shannon is considered by many to be the “father of information theory.” His seminal work, the 1948 paper “A Mathematical Theory of Communication,” laid the foundation for information theory, transforming the understanding of data encoding in communication systems. In this theory, Shannon introduced the concept of entropy, a measure of uncertainty or randomness in information, which has since become a cornerstone in various fields, including cryptography, data compression, and telecommunications.

Shannon Entropy in Cryptography

Shannon entropy is a measure of the unpredictability or the randomness of information content. In the context of cryptography, particularly at a senior college level, Shannon entropy plays a crucial role in assessing the security and effectiveness of cryptographic systems.

Shannon entropy in cryptography is about assessing and ensuring the unpredictability and randomness within cryptographic systems. It’s a critical parameter in evaluating the security of cryptographic keys and algorithms, serving as a benchmark for the strength and robustness of cryptographic methods. Understanding and applying the concept of entropy allows for the design of more secure cryptographic systems.

The Shannon entropy \(H(X)\) of a discrete random variable \(X\) with possible values \({x_1, x_2, ..., x_n}\) and probability mass function \(P×\) is defined as:

\(H(X) = -\sum_{i=1}^{n} P(x_i) \log_2 P(x_i)\)

In this formula, \(P(x_i)\) is the probability of the random variable taking a specific value \(x_i\), and the logarithm is base 2, reflecting the binary nature of information encoding. The result is a measure in bits. For example, \(x\) could refer to a character that can occur in a document and \(P(x)\) the ratio of the number of occurrences of that character to the total number of characters. \(log_2\) of that tells us the number of bits needed to represent them.

Measuring entropy is a key part of developing data compression algorithms (e.g., Huffman coding). Instead of representing all characters with same number of bits, we can use variable-length values where frequently occurring characters (or bytes, in the general case) can be encoded with a small number of bits and less-frequently occurring characters with more bits. This can be extended to multi-byte sequences as well.

In cryptography, entropy is used to quantify the amount of randomness or uncertainty in a system. High entropy implies high unpredictability, which is desirable for cryptographic keys. A key with high entropy is harder to guess or brute-force.

Entropy can be used to measure how much information about the plaintext may be leaked by the ciphertext. The goal of a secure encryption algorithm is to ensure that the ciphertext reveals minimal or no information about the plaintext or the encryption key. We want to see high entropy in ciphertext.

Let’s consider the simple entropy of plain text documents. If we assume all letters were equally probable and the document only contains 26 letters (i.e., remove whitespace and non-alphabetic characters and convert upper-case to lowercase) then the entropy of the document would be \(log_2(26) = 4.70\) bits. This should make intuitive sense since 2⁴ is 16, which tells us that four bits aren’t enough to hold 26 characters, and 2⁵ is 32, which gives us more space than we really need. We certainly don’t need all eight bits of each byte. When we look at real text, we see slightly lower entropy. The text of Moby Dick has an entropy of 4.175 bits and the complete works of Shakespeare has an entropy of 4.19 bits.

Cryptographic algorithms, particularly those involving random number generation, rely on high entropy sources to ensure unpredictability in their outputs. The security of cryptographic protocols like key exchanges, digital signatures, and encryption schemes depends significantly on the entropy of the underlying random processes. Note that a high entropy does not necessarily mean we have a secure cipher, but it does mean we have more randomness, so we do want our ciphertext to have high entropy. Data compression algorithms generate output with high entropy but are not cryptographic.

Polyalphabetic Substitution Ciphers

The simplicity of monoalphabetic substitution ciphers eventually became their downfall, as they were easily broken through frequency analysis. This technique exploits the fact that the entropy and frequency distribution of the ciphertext in these ciphers match those of the plaintext.

To counter this vulnerability, a more advanced method was needed, one that would vary the mapping of plaintext letters to ciphertext letters throughout the message. For instance, the letter ‘A’ in the plaintext could initially be encoded as ‘G’, then later as ‘E’, and even later as ‘C’. This variation would effectively disrupt the pattern that frequency analysis relies on and increase the entropy of the ciphertext.

Enter Leon Battista Alberti, an Italian scholar and artist, around 1466. Alberti developed the polyalphabetic substitution cipher, marking a significant leap in the field of cryptography. In a polyalphabetic cipher, the translation of a plaintext letter to a ciphertext letter changes depending on the letter’s position in the text. This method significantly complicates frequency analysis, making the cipher much harder to crack.

Alberti’s contributions to cryptography were so groundbreaking that he’s often hailed as “the father of western cryptography.” He not only invented the polyalphabetic cipher but also authored the first letter frequency table, which ironically made it easier to break monoalphabetic ciphers.

Alberti also designed a cipher disk to facilitate the encoding process. This disk consisted of two parts: an outer ring displaying the alphabet and numbers 1 through 4, and an inner wheel with letters in a scrambled order alongside a few symbols. The inner wheel could be rotated relative to the outer ring during the encoding of a message, implementing the polyalphabetic substitution in a practical and efficient manner.

Alberti Cipher: The Mechanics of the First Polyalphabetic Cipher

The Alberti Cipher, named after its inventor Leon Battista Alberti, is a seminal creation in the history of cryptography. This cipher employs a simple yet ingenious mechanism using two disks - an outer disk and an inner disk - to encrypt text.

To begin encryption with the Alberti Cipher, you align a specific character on the outer disk with a specific character on the inner disk. For instance, you might line up the letter ‘A’ on the outer disk with the letter ‘g’ on the inner disk. The outer disk represents the plaintext (the original message), while the inner disk contains the ciphertext characters (the encoded message).

In this setup, if ‘A’ aligns with ‘g’, then ‘A’ in the plaintext would be encrypted as ‘g’ in the ciphertext. Similarly, ‘B’ might align with ‘k’, and so forth. The key to the Alberti Cipher’s effectiveness lies in the ability to rotate the inner disk. By rotating it one position clockwise, the encryption of each letter changes. For example, after one rotation, ‘A’ would no longer encode to ‘g’ but might encode to ‘e’ instead.

A common method of encryption was to agree upon a starting position and then rotate the inner disk by one position after encrypting a set number of characters. This method adds a layer of complexity to the encryption process, making the cipher more secure.

There were various techniques to signal when to rotate the disk. Some methods involved using a specific number or a reserved letter within the message as a cue to rotate the disk.

Interestingly, the legacy of the Alberti Cipher lives on today in a more playful form – the secret decoder rings, often found in children’s games and spy kits, are a direct descendant of Alberti’s revolutionary invention.

Vigenère Cipher

The Vigenère cipher, named after the renowned 16th-century cryptographer Blaise de Vigenère, is a significant development in the history of cryptography. Introduced in 1585, the Vigenère cipher gained fame for its simplicity and effectiveness, particularly in military applications, which were the primary focus of cryptography until the late 1960s.

What set the Vigenère cipher apart was not the invention of a new mechanism; rather, it was Vigenère’s innovative approach to using keys. This cipher was celebrated for its perceived unbreakability and remained a cipher of choice for several centuries. It continues to be a viable option for pencil-and-paper cryptography in field situations due to its simplicity and does not require any specialized hardware like a cipher disk.

To use the Vigenère cipher, you start by creating a table known as a Vigenère square or tabula recta. This table consists of the alphabet written out 26 times in different rows, each row shifted one letter to the left compared to the row above it. Essentially, this table includes all possible Caesar cipher shift alphabets.

The next step is choosing a key. The Vigenère cipher uses a repeating key - the key is repeated to match the length of the message being encrypted. This repeated key is a simple form of a keystream. A keystream produces an arbitrarily long key sequence based on some initial starting key. For example, if you choose the key “FACE”, the keystream for the message would be a repetition of this key, extended to the length of the message: “FACEFACEFACEFA…”. This method of encryption provides a more secure approach, as it significantly complicates the process of deciphering the message without knowledge of the key and enables greater security with a longer and more complex key. Modern algorithms that use keystreams use far more sophisticated pseudorandom number generators.

Vigenère encryption

To encrypt, we locate the row that is indexed by the keystream character. Then we find the column that contains the plaintext character. The intersection is the ciphertext. To decrypt, we do the reverse: we locate the row that is indexed by the keystream character and then search that row for the column that contains the ciphertext character. The heading of the column tells us the plaintext letter.

With this cipher, each letter of the key selects a different substitution cipher. A message will be encrypted with as many substitution ciphers as there are unique letters in the keyword.

The Vigenere cipher was used during the U.S. Civil War. One of the problems encountered with a polyalphabetic cipher is that the encoding of a character depends on its position in the text. If you gain or lose a character or just make a mistake, everything is thrown off for future characters. This is a quote from someone who had to experience it during the war:

“In practice, it proved a dismal failure. For one thing, transmission errors that added or subtracted a letter … unmeshed the key from the cipher and caused no end of difficulty.”

Cryptanalysis of the Vigenère cipher

The Vigenère cipher, long considered unbreakable, stood as a formidable challenge in cryptanalysis for centuries. Breaking this cipher involves a two-part process.

The first step is to determine the length of the key. One common technique involves searching for repeating groups of letters throughout the ciphertext. These recurring sequences in different parts of the ciphertext are known as coincidences.

By examining the distances between these repeated patterns, cryptanalysts can gain insights into the possible key length. They plot various key lengths and observe which ones yield the highest number of coincidences. This method helps to narrow down the probable length of the key used in the cipher.

Once a plausible key length is identified, the process shifts to treating the ciphertext as if it were encoded with multiple Caesar ciphers. For instance, if the guessed key length is 7, then every 7th character (1st, 8th, 15th, 22nd, 29th, etc.) is encoded using the same shift. Cryptanalysts can extract these sequences and apply frequency analysis, similar to breaking a Caesar cipher.

This method of breaking the Vigenère cipher revolves around analyzing patterns and frequencies, exploiting the inherent weaknesses of the cipher’s structure, especially its repetitive use of the key.

One-Time Pad: The Unbreakable Cipher

In 1917, cryptography took a monumental leap forward with the invention of the one-time pad. To this day, it remains the only encryption method that is provably secure. While other ciphers, no matter how complex, could potentially be cracked given enough computing power and time, the one-time pad stands apart as unbreakable.

The concept of the one-time pad is straightforward. It involves using a long, non-repeating sequence of completely random key letters. These letters are used only once (hence the name “one-time pad”) and were originally written on a pad of paper. In some cases, they were even written on cellulose-nitrate film, which is highly flammable, allowing for easy and secure disposal.

The fundamental rule of the one-time pad is that each letter in the key is used to encrypt exactly one letter of the plaintext. The encryption process is a simple matter of adding the two characters' values, modulo the alphabet size. For instance, in this system, ‘A’ is considered 0, ‘B’ is 1, ‘C’ is 2, and so on. So, encrypting ‘B’ with ‘B’ would result in ‘B’+‘B’ = 1+1 = 2 = ‘C’.

Once a portion of the key is used for encryption, it is destroyed by the sender, ensuring that it can never be reused. This practice is essential for maintaining the integrity of the system. The recipient of the message uses an identical pad to decrypt the message, following the same procedure in reverse.

It’s very easy to use one-time pads in computers with binary data. We need a key that is as long as the message and simply exclusive-or each byte of plaintext with a byte of the key. The receiver would need to have the same key to decrypt the message. Here’s some C code that will do the job:

void onetimepad(void)
{
	FILE *if = fopen("intext", "r");
	FILE *kf = fopen("keytext", "r");
	FILE *of = fopen("outtext", "w");
	int c, k;

	while ((c = getc(if)) != EOF) {
		k = getc(kf);
		putc((c^k), of);
	}
	fclose(if); fclose(kf); fclose(of);
}

We read bytes from our plaintext and key files and write a file named outtext, which is our ciphertext. Each output byte is the next byte from the plaintext exclusive-ored with the next byte from the key. The exact same code accomplishes encryption as well as decryption.

Perfect secrecy

One-time pads are renowned for providing what’s known as perfect secrecy in the realm of information theory. Perfect secrecy has these properties:

1. The ciphertext reveals no information about the content of the plaintext or the key. Of course, it does not hide the fact that a message exists.
2. Given several plaintexts, you will have no way of determining which one created the cipher text (this is the property of indistinguishability).
3. You can always create some key that will convert any ciphertext to any possible plaintext.

See this video for an explanation of perfect secrecy.

However, achieving perfect secrecy comes with its own set of practical challenges:

Key Length: For perfect secrecy, the key must be as long as the message itself. This means if you’re encrypting a 20 GB video, the key also needs to be 20 GB. This requirement makes key storage a significant issue, as you need enough storage for keys equal in size to all the messages you intend to encrypt.

Key Distribution: The distribution of keys poses another major hurdle. Every recipient who needs to decrypt the message must have the exact same key, and this key must be as long as the message. This creates a paradoxical situation where securely delivering a long key becomes as challenging as delivering the message itself.

Random Key Generation: The keys must be generated in a completely random manner. Any discernible pattern in the key sequence could potentially be exploited, compromising the encryption.

Key Reuse: The security of the one-time pad is utterly compromised if keys are reused. Every new piece of data must be encrypted with a key sequence that has never been used before.

Synchronization of Sender and Receiver: Both the sender and receiver must use the exact same key sequence and be perfectly synchronized in its use. Historically, messages could indicate which page of the pad to start on, but in the digital age, ensuring that both parties start decrypting at the exact point in the key sequence is crucial and can be complex.

While one-time pads offer unparalleled security in theory, these practical limitations restrict their use to very specific, high-security scenarios. The balance between perfect secrecy and practical applicability remains a key consideration in the use of this encryption method.

Random Numbers in Cryptography

Random numbers play a crucial role in cryptography. The goal of encryption is to produce an outcome that resembles a uniformly random distribution of bits, making the encrypted data indistinguishable from random noise.

In cryptography, a symmetric key essentially is a random number. This is particularly evident in one-time pads, where the requirement for long, completely random keys is paramount. A lack of randomness in cryptographic operations would lead to predictability, undermining the security of the encryption. Random numbers are also used to generate authentication challenges, TCP starting sequence numbers, starting points for allocating different parts of memory, and any other uses where unpredictability is important to guard against attacks.

Predictable Random Keys

An example of exploiting non-randomness in generating a random key is a May 2024 recovery of a key in a crypto wallet [Wired article]. The owner of 43.6 bitcoin stored the password for his digital wallet in a file encrypted with TrueCrypt, which is file encryption software. The file was corrupted and he could no longer retrieve his 20-character password , which was generated via a RoboForm password manager but not stored in the password manager.

The owner contacted Joe Grand, a hardware hacker, to help retrieve the key. Running a script to try all combinations of 20-character passwords would not be feasible: it would take way too long. Grand and his friend Bruno reverse-engineered the password generator in RoboForm and discovered flaws in the random number generator. The pseudorandom number generation that was used to generate passwords was initialialized from the date and time on the user’s computer.

The owner didn’t know the date but they found the year and a guessed a range of a bit over a month based on when the bitcoin was moved to the wallet. That reduced the possible set of passwords dramatically and they eventually were able to find the correct password. Joe Grand created a video to describe their efforts: I hacked time to recover $3 million from a Bitcoin software wallet.

Generating Random Numbers

John von Neumann, a leading 20th-century mathematician and a pioneer in computer science, famously stated in 1951, “Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin.” This highlights the complexity and importance of generating truly random numbers.

Contrary to popular belief, many computer-based random number libraries, like the rand() function in Linux, don’t produce actual random numbers. Instead, they are pseudo-random number generators. These generators start with a seed value and produce a sequence that appears random. However, the same sequence will always be generated from the same seed, resulting in a semblance of randomness rather than genuine randomness. They are specifically designed to be deterministic. Common techniques for pseudo-random number generation include:

• Linear feedback shift registers
• Multiplicative lagged Fibonacci generators
• Linear congruential generators

Programmers often use pseudorandom number generators to simulate a random number generator by seeding it with random data. For true randomness, sources of high entropy are sought. Entropy, in this context, is a measure of unpredictability or randomness in events. High entropy is desired as it equates to greater unpredictability.

Sources of randomness can include:

• Measuring time intervals between keystrokes
• Observing network or kernel events, such as the timing of interrupts
• Cosmic rays
• Electrical noise
• Analyzing encrypted messages or their checksums
• Lava lamps (see this article on how Cloudflare uses a wall of lava lamps to generate random numbers)

In fact, random numbers are so crucial to computing that Intel has provided a Digital Random Number Generator (DRNG) in their processors since 2018 that uses a processor resident entropy source. ARM architectures also provide randomness. ARM’s TrustZone security engine contains a True Random Number Generator.

In Linux systems, two devices, /dev/random and /dev/urandom, are provided to generate random numbers. /dev/random offers high-quality randomness, dispensing data only when there is a sufficient amount of entropy. Conversely, /dev/urandom was dewsigned to provides data without a delay, though the randomness quality may vary depending on the rate of data consumption. It used a high-entropy random data to feed a pseudo-random number generator.

Starting with the Linux 5.17 and 5.18 kernels, the two pseudo-devices are now equivalent. The random driver actively adds entropy using the processor’s cycle counter, measuring the elapsed time after running the scheduler, if it doesn’t have sufficient entropy.

Similarly, security-specific coprocessors, such as ARM’s TrustZone and Apple’s Secure Enclave, also include true random number generators.

Electromechanical Cryptographic Engines: Rotor Machines

Moving into the 20th century, cryptography underwent a significant transformation with the introduction of electromechanical devices. This innovation marked a departure from the traditional methods that relied on pencil-and-paper computations. The 1920s saw the rise of mechanical devices designed to automate the encryption process. These devices, known as rotor machines, featured a series of independently rotating cylinders or rotors, through which electrical pulses were transmitted.

Each rotor in these machines was equipped with input and output connectors for each letter of the alphabet. The connections between input and output were scrambled, meaning each rotor effectively implemented a substitution cipher. When multiple rotors were used in sequence, they collectively executed a more complex version of the Vigenère cipher.

The Single Rotor Machine

The simplest form of a rotor machine uses just one rotor. Inside this rotor, a set of wires connected input character positions to output character positions. With each character entry, the rotor would rotate by one position, shifting all internal connections accordingly. Thus, a single rotor machine functioned as a polyalphabetic substitution cipher, repeating every 26 characters for an alphabet of that length.

Visualizing the internal workings of a single-rotor machine can be challenging. If we were to unfold the rotor, we would see how each input and output connection is made. After entering a character, these connections shift by one position. For example, a connection initially linking ‘Y’ to ‘W’ would change to connect ‘Z’ to ‘X’. The substitution alphabet, therefore, alters with each rotation.

Multi-Cylinder Rotor Machines

To overcome the limitation of predictability after 26 characters, rotor machines were designed with multiple cylinders. The output of one rotor fed into the next. The first rotor advanced after each character entry, while the second rotor moved only after the first rotor completed a full rotation. This system significantly extended the repetition period of the substitution cipher.

For instance, a three-rotor machine with a 26-character alphabet wouldn’t repeat its substitution alphabet until 17,576 (26³) characters were entered. With five rotors, this number increased to over 11 million (26⁵) characters.

Enigma: The Iconic Rotor Machine of WWII

The Enigma machine, the most renowned rotor machine, was used by Germany during World War II. It is particularly famous for its complexity and the role it played in wartime communications.

The Enigma utilized three rotors, creating over 17,000 different positions before its substitution alphabet would repeat. This level of complexity made it an incredibly secure system at the time. The machine’s encryption process began with an input data permutation via a patch panel, which was then fed into the rotor engine.

A distinctive feature of the Enigma was its reflector disk. Data, after passing through the last rotor, was sent to this disk, which then reflected the electrical connections back through the rotors in reverse. This design didn’t necessarily strengthen the encryption but made it symmetric. Symmetry meant that if the receiving party set their Enigma machine to the same initial settings, typing in the ciphertext would reveal the plaintext.

For effective communication, both sides needed to agree on these initial rotor settings. These settings were typically determined by a function of the date and were listed in a codebook.

Cracking the Enigma cipher was a monumental task accomplished by the team at Bletchley Park, building upon earlier work by the Polish Cipher Bureau. The challenge lay in deducing the internal wiring of the rotors and determining the starting positions of these rotors for a given message.

The task was somewhat eased by certain operational habits, such as the infrequent changing of rotor order and the common practice of starting messages with the letters “ANX” (“AN” being the German word for “to,” with “X” used as a space). Also, because of the design of the reflector, a ciphertext character is guaranteed to be different from a plaintext character for every substitution alphabet. These patterns provided crucial clues that assisted in deciphering the Enigma’s encryption.

Transposition ciphers

We just covered substitution ciphers. Another family of classic ciphers is transposition ciphers. In a transposition cipher, we don’t replace characters but rather shuffle them around. Knowing how to unshuffle them allows us to decrypt the message.

Because the characters in the data don’t change, the frequency distribution remains the same. However, transposition splits common letter sequences to increase the entropy of digraphs and trigraphs in the plaintext.

The skytale

The skytale (pronounced like ‘Italy’) is a classic example of an ancient cipher. It requires a rod of a specific width around which a strip of paper is wrapped.

To encrypt a message using the skytale, you write the message on a long, narrow strip of paper. This paper strip is then wound around the rod. The crucial aspect of this cipher is the width of the rod, which determines how the letters align when the paper is wrapped around it. The encrypted message is then read along the length of the rod.

Let’s go through an example using the phrase “MY CAT HAS FLEAS.” By wrapping this message around the rod and reading down the length of the rod, a new sequence of text is produced, forming the encrypted message.

An important factor in this method is ensuring that the text length is an even multiple of the number of characters that can be read along the rod’s length. If the text doesn’t fit this requirement, it must be padded. Padding involves adding extra, non-essential text to the end of your message, ensuring that it fits perfectly around the rod. This makes the text the correct length to be encrypted by the skytale cipher. Padding is essential for block ciphers, which encrypt chunks of data at a time.

Skytale as a set of columns

We can simulate the staff with a table. In the table version, we enter text into a fixed-width table, wrapping to new rows as necessary.

We then add padding to any empty cells and read the results column by column.

Here’s an example. We entered “MY CAT HAS FLEAS xy” into the table. Now we read the data starting from the first column and then moving on to subsequent columns. We can the same results as before. The secret to decryption here is knowing the width of the table.

Even though the skytale is not vulnerable to frequency analysis, the ciphertext is trivial to attack. You simply make all possible matrices that would fit the ciphertext. Then you write ciphertext across the rows and see if the columns contain legible content.

Columnar transposition

We can make the cipher more difficult by adding a key that will tell us the width of the table and the order to read columns to generate the ciphertext instead of starting from the leftmost column. The key will contain unique characters and the sorting sequence of the characters determines the sequence in which we will read the columns. For example, if the key is the word FARE, the sorting sequence will be 3, 1, 4, 2.

We read the column corresponding to 1 first. Then the column corresponding to 2. Then the column for 3., and finally, the last column to get all of our ciphertext.

Scrambled columns make the ciphertext a bit harder to crack but not much. The same technique is applied as before - testing columns of text with rows of different sizes. But now we can look for plausible combinations of text that spans from the end of one column to the start of the next one. This focuses on finding likely digraphs and trigraphs.

Combined ciphers

Transposition ciphers on their own were never too popular. The biggest problem was that they required holding on to intermediate results. For instance, you need to store the entire message before you can output any of the ciphertext.

For decrypting, you need to receive the entire message before you can begin to decrypt it. This was particularly troublesome with pencil-and-paper cryptography but also required storing contents in memory for computer cryptography. Transposition ciphers were sometimes combined with substitution ciphers, such as a German cipher used during World War I but they never achieved widespread use. However, the idea behind them is good. Substitutions increase the entropy of text and transpositions increase the entropy of digraphs and trigraphs. Many modern ciphers use a combination of substitutions and transpositions (permutations).

Modern ciphers

While one-time pads have been regularly used on computers and there have been software implementations of rotor machines, computers give us the ability to play around with bits to a degree we cannot do with pencil and paper or mechanical devices and achieve far stronger levels of encryption.

Computer cryptography also enables us to look at bits instead of text characters, allowing us to encrypt arbitrary content.

Kerckhoffs’s Principle is the guiding principle in cryptography: secrecy resides in the key. It allows us to study algorithms that are actually used rather than hoping to reverse-engineer proprietary algorithms.

Confusion and diffusion

Claude Shannon defined two desirable properties for the operation of a cipher: confusion and diffusion.

Confusion

Shannon proposed that a well-designed cipher should have a property he called confusion. This means that there is no obvious or direct correlation between any bit of the key and the resulting ciphertext. In a state of perfect confusion, every bit of ciphertext is influenced by multiple bits of the key, obscuring any direct connection between the two. This is typically achieved through substitution methods.

Diffusion

The second principle, ‘diffusion’, takes the information from the plaintext and scatters it across the cipher. Shannon’s vision was that a change in just one bit of plaintext should, on average, alter about half of the ciphertext’s bits. This principle is usually put into practice through transposition methods. Diffusion’s goal is to complicate the relationship between the plaintext and ciphertext as much as possible, ensuring that the original message is dispersed throughout the cipher, leaving no trace of patterns or structure.

Shannon’s approach to encryption - with confusion adding complexity to the key-ciphertext relationship, and diffusion entangling the plaintext information within the cipher - has set the standard for secure communication.

Stream ciphers

Symmetric key ciphers fall into two categories: stream and block ciphers.

A stream cipher simulates a one-time pad by using a keystream generator to create a set of key bytes that is as long as the message. A keystream generator is a pseudorandom number generator that is seeded, or initialized, with a key that drives the output of all the bytes that the generator spits out.

The keystream generator is fully deterministic: the same key will produce the same stream of output bytes each time. Because of this, receivers only need to have the key to be able to decipher a message. With that, they can generate the same key stream.

However, because the keystream generator does not generate true random numbers, the stream cipher is not a true substitute for a one-time pad. Its strength rests solely on the strength of the key. A keystream generator will, at some point, will reach an internal state that is identical to some previous internal state and produce output that is a repetition of the previous output. This also limits the security of a stream cipher. Since key repetition may not occur for a long time, stream ciphers can still be useful in many applications.

The ChaCha20 stream cipher

ChaCha20 is a high-speed stream cipher designed by Daniel J. Bernstein. It operates by generating a keystream of small pseudo-random bits from a secret key and a nonce (a number that should only be used once). This keystream is then XORed with the plaintext to produce ciphertext – each successive byte of the keystream is XORed with each successive byte of the plaintext. Decryption uses the exact same process.

The cipher is known for its simplicity and high performance, particularly in software implementations. Its low overhead makes it an attractive choice for low-power or low-performance devices.

ChaCha20 has been shown to provide substantial resistance to cryptanalysis and has been widely adopted in various encryption protocols, including serving as one of the accepted cipher for securing web traffic as part of TLS (Transport Layer Security) as well as providing secure network connections in some VPNs. While the operation of XORing is trivially simple, the magic of ChaCha’s security lies in its keystream generator.

Block ciphers

Most modern symmetric ciphers in use today are block ciphers, meaning that they encrypt a chunk of bytes, or a block, of plaintext at a time. The same key is used to encrypt each successive block of plaintext. AES and DES are two of the most popular symmetric block ciphers. Common block sizes are 64 bits (8 bytes, used by DES) and 128 bits (16 bytes, used by AES). Note that the block size does not necessarily relate the the key size.

S-boxes, P-boxes, and encryption networks

Block ciphers are often implemented using an SP Network, which stands for substitution-permutation network. These are designed to create the properties of confusion and diffusion in ciphertext.

Confusion and diffusion are generated in constructs called s-boxes and p-boxes. An s-box (Substitution box) performs an invertible operation that replaces (substitutes) one set of bits with another set of bits; it takes an input and, based on a fixed or dynamic table of values, transforms it into an output, playing a critical role in the confusion aspect of encryption by obscuring the relationship between the key and the ciphertext.

A p-box (Permutation box) is a method used in block ciphers to perform transposition, systematically rearranging the order of the bits in the data blocks, thereby contributing to diffusion by spreading the influence of a single plaintext bit over many ciphertext bits.

Block ciphers iterate through multiple **rounds*. Each round performs a partial encryption. These rounds can take one of two forms: a Feistel Network (Feistel cipher) or a Substitution-Permutation Network (SP Network, or SPN). Multiple rounds are used because a single round does not provide perfect confusion or diffusion.

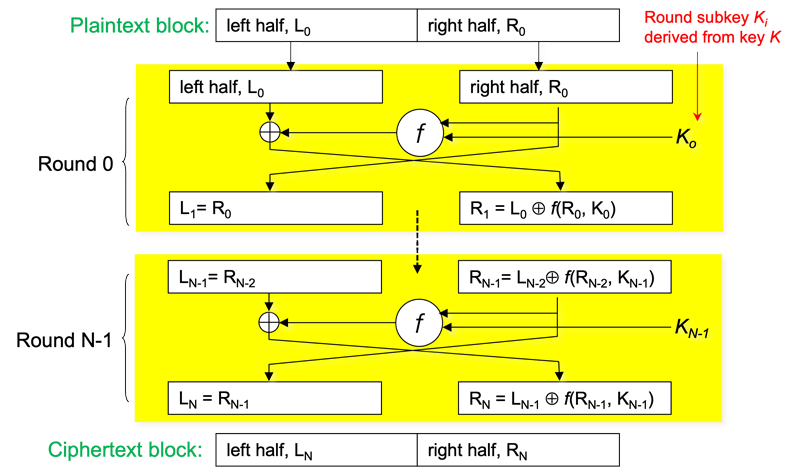
Feistel Network

Encryption must be an invertible operation. That is, you must be able to decrypt what you encrypted (providing you have the key, of course). The Feistel network was designed to provide a mechanism that can use any function, even a non-invertible one, within a round and still create an invertible cipher.

In a cipher that uses a Feistel Network, the plaintext block is split into two equal parts: a left part (L₀) and a right part (R₀). Each round produces a new left and right block that are fed into the next round.

In each round, only half of the data block is encrypted by a round function, which takes as input a subkey for that round and the right part of the block. The result is then XORed with the left half of the data (L₀ ⊕ R₀). This result then becomes the new right part while the original right part becomes the left part for the new round:

R₁ = L₀ ⊕ R₀
L₁ = R₀

The part that wasn’t encrypted in the previous round gets encrypted in the next round.

Substitution-Permutation Network (SPN)

An SP Network (SPN) encrypts a block of plaintext through several rounds (iterations). Each round applies a degree of confusion and diffusion to the input to create intermediate ciphertext. The operation of the s-boxes (what to substitute) and p-boxes (what to scramble) is driven by a subkey, also known as a round key. This is a key that is derived from the original key in a different way for each round. This allows, for instance, an s-box to reference a different table of substitutions for each subway.

DES

The Data Encryption Standard (DES) originated from an earlier cipher named Lucifer, developed by Horst Feistel at IBM. In response to the increasing commercial and national security needs for secure data transmission, the U.S. government recognized the need for a robust, standardized encryption method. IBM, with modifications and input from the National Security Agency (NSA), adapted Lucifer into what would become DES. This transformation involved reducing the key size from 64 to 56 bits and redesigning the s-boxes used by the algorithm. Officially adopted in 1977, DES was the first commercially-available strong cipher and ushered in an era where cryptography was no longer the realm of national intelligence agencies.

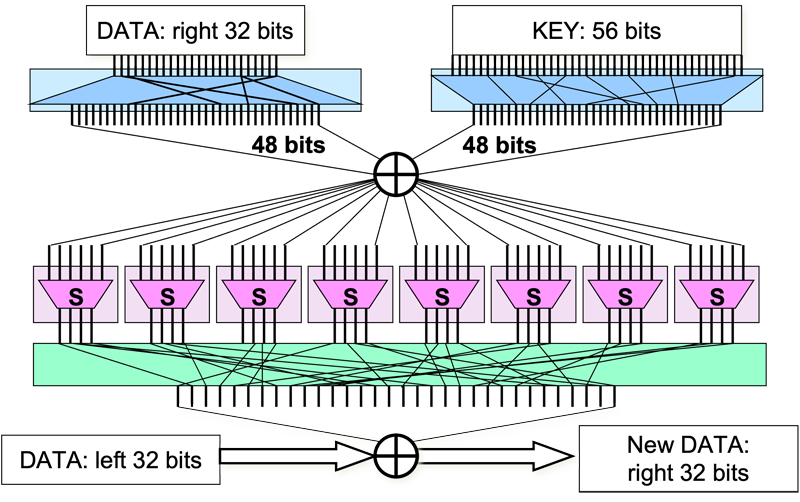
DES based on the Feistel cipher and encrypts 64-bit blocks using a 56-bit key. Instead of using an SP Network, it uses a Feistel Network.

It starts with an initial permutation that scrambles the 64 bits of the block before going through 16 rounds of the Feistel network. At the end, another permutation, that is the inverse of the initial permutation, is applied to the block.

Within each round, the encryption function on each half block does the following:

1. The right half of the block goes through an expansion permutation where 32 bits of data are permuted and expanded into 48 bits.
2. 48 bits are generated from the key through permutation, inversion, and selection
3. These two values are XORed together
4. Each set of 6 bits passes through an s-box that converts 6 bits of input to 4 bits of output. Normally, this would imply that data would be lost but note that in the end the eight s-boxes produce 32 bits of data, the same as the input.
5. The resulting 32 bits of data go through a permutation and are XORed with the left half of the block (which was untouched this round).

The permutations and substitutions are guided by the subkey for that round. A core component of the security of DES is its design of the s-box, which converts the 6 input bits to 4 output bits and adds confusion by altering the relationship between the input and output bits.

DES has been shown to have some minor weaknesses against cryptanalysis. A key can be recovered using 2⁴⁷ chosen plaintexts or 2⁴³ known plaintexts. Note that this is not a practical amount of data to get for a real attack. The major weakness of DES is not the algorithm but its 56-bit key. An exhaustive search requires 2⁵⁵ iterations on average (we assume that, on average, the plaintext is recovered halfway through the search). This was an insurmountable amount of computing for computers in the 1970s but is not much for today. Custom hardware (FPGA-based DES crackers) or distributed efforts can do an exhaustive search to crack a DES key within a day.

Triple-DES

Triple-DES (3DES) solves the key size problem of DES and allows DES to use keys up to 168 bits. It does this by applying three layers of encryption:

1. C' = Encrypt M with key K₁
2. C'' = Decrypt C' with key K₂
3. C = Encrypt C'' with key K₃

If K₁, K₂, and K₃ are identical, we have the original DES algorithm since the decryption in the second step cancels out the encryption in the first step. If K₁ and K₃ are the same, we effectively have a 112-bit key and if all three keys are different, we have a 168-bit key.

Cryptanalysis has not been effective against 3DES: the three layers of encryption use 48 rounds instead of 16 making it infeasible to reconstruct the functions of the s-boxes.

DES is relatively slow compared with other symmetric ciphers, such as AES. It was designed with hardware implementations in mind. Moreover, 3DES is, of course, three times slower than DES. There is no good reason to use DES anymore.

AES

AES, the Advanced Encryption Standard, was chosen as a successor to DES and became a federal government standard in 2002. It uses a larger block size than DES: 128 bits (16 bytes) versus DES’s 64 bits (8 bytes) and supports larger key sizes: 128, 192, and 256 bits. Note that even 128 bits are long enough to resist brute-force searches.

The 128-bit block of data passes through multiple rounds of encryption. Each round uses a subkey derived from the encryption key and performs the following operations:

Step 1: Byte Substitution (s-boxes)

AES begins with the byte substitution step, where each of the 16 input bytes is substituted using a predefined table known as an s-box. This step is designed for confusion, replacing each byte with another according to the s-box, which is a non-linear substitution table that ensures that the output is not directly proportional to the input. The result of this substitution is organized into a 4x4 matrix.

Step 2: Shift Rows

The next step involves shifting rows in the matrix to the left, with different offsets for each row. This process creates diffusion in the ciphertext. The first row is not shifted, the second row is shifted one position to the left, the third row two positions, and the fourth row three positions. This shifting means that each row of the matrix is reordered, further scrambling the data.

Step 3: Mix Columns

During the mix columns step, AES performs a matrix multiplication on each column of the 4x4 matrix, effectively transforming each column based on the values of all four bytes in the column. This further disperses the plaintext bits over the ciphertext, adding to the diffusion.

Step 4: XOR Round Key

Finally, the 128 bits of the round key are XORed with the 16 bytes of the matrix from the previous step. This incorporates the key into the encrypted data, with each round using a different key derived from the initial key.

These steps (excluding Mix Columns in the final round) are repeated for a number of rounds—10, 12, or 14, depending on the key size (128, 192, or 256 bits respectively). Each round builds upon the security of the previous one, making AES resilient against various attack strategies.

The block passes through s-boxes that substitute one set of bits for another via a table lookup, with the table selected by the subkey for the round. The resulting block is scrambled via a permutation that is also guided by the subkey.

No significant academic attacks against AES have been discovered thus far beyond brute force search. AES also has the advantage that it is typically 5–10 times faster in software than 3DES.

Block cipher modes

Electronic Code Book (ECB)

When data is encrypted with a block cipher, it is broken into blocks and each block is encrypted separately. This leads to two problems.

1. If different encrypted messages contain the same substrings and use the same key, an intruder can deduce that it is the same data.

2. Secondly, a malicious party can delete, add, or replace blocks (perhaps with blocks that were captured from previous messages).

This basic form of a block cipher is called an electronic codebook (ECB). Think of the codebook as a database of encrypted content. You can look up a block of plaintext and find the corresponding ciphertext. This is not feasible to implement for arbitrary messages but refers to the historic use of codebooks to convert plaintext messages to ciphertext.

Cipher Block Chaining (CBC)

Cipher block chaining (CBC) addresses these problems. Every block of data is still encrypted with the same key. However, prior to being encrypted, the data block is exclusive-ORed with the previous block of ciphertext. The receiver does the process in reverse: a block of received data is decrypted and then exclusive-ored with the previously received block of ciphertext to obtain the original data. The very first block is exclusive-ored with a random initialization vector, which must be transmitted to the remote side.

Note that CBC does not make the encryption more secure; it simply makes the result of each block of data dependent on all previous previous blocks so that data cannot be meaningfully inserted or deleted in the message stream.

Counter mode (CTR)

Counter mode (CTR) also addresses these problems but in a different way. The ciphertext of each block is a function of its position in the message. Encryption starts with a message counter. The counter is incremented for each block of input. Only the counter is encrypted. The resulting ciphertext is then exclusive-ORed with the corresponding block of plaintext, producing a block of message ciphertext. To decrypt, the receiver does the same thing and needs to know the starting value of the counter as well as the key.

An advantage of CTR mode is that each block has no dependence on other blocks and encryption on multiple blocks can be done in parallel.

Cryptanalysis

Cryptanalysis is the study of analyzing and breaking cryptographic systems to retrieve the original message without having access to the secret key. The goal is to find some systematic non-random behavior within an encryption algorithm that can be exploited more efficiently than performing an exhaustive search across all possible keys.

Let’s go over some of the fundamental types of attacks in trying to break codes:

1. Brute-force Attack

A brute-force attack is the simplest form of attack in cryptography. It involves trying every possible key until the correct one is found.

Example: Suppose a message is encrypted using a Caesar cipher with an unknown shift. A brute-force attack would try every possible shift (from 0 to 25) to decrypt the ciphertext until the meaningful plaintext is found. For modern algorithms like AES-128, brute-forcing would require trying all \(2^{128}\) (\(3.40282 \times 10^{38}\)) possible keys, which is computationally infeasible with current technology.

2. Known-plaintext Attack

A known-plaintext attack occurs when the attacker has access to both the ciphertext and the corresponding plaintext for some portion of the communication. The attacker can use this information to deduce the encryption key or decipher other messages encrypted with the same key. This attack is based on the assumption that the attacker has somehow obtained some pairs of plaintexts and ciphertexts, perhaps through espionage or other means. Historical cryptanalysis, often involved known plaintext attacks. It doesn’t mean that the entire plaintext is known but some portion may be deduced (e.g., a date or greeting at the start of a message or standard headers).

Example: During WWII, the German Enigma machine was vulnerable to known-plaintext attacks. Allied cryptanalysts would sometimes know the plaintext of certain messages (such as weather reports) and use this information to help break the encryption for other messages.

3. Chosen-plaintext Attack

In a chosen-plaintext attack, the attacker can choose arbitrary plaintexts to be encrypted and obtain the corresponding ciphertexts. This helps the attacker study how plaintexts are transformed into ciphertexts and potentially deduce the encryption key.

Example: In the case of a block cipher like AES, if the attacker can submit specific plaintexts for encryption (like sending known messages to a secure server and observing the encrypted responses), they may gain insights into the structure of the encryption algorithm and deduce the key or crack the cipher. As with known-plaintext attacks, the attacker may not be able to get a complete message encrypted. Historically, in wartime, an attacker might create some activity in a new place, knowing that the enemy will likely mention it in their reports. For instance, creating something noteworthy in the town of Gschlachtenbretzingen, Germany could give the analyst a lucky feeling that Gschlachtenbretzingen is encoded in the next briefing.

4. Ciphertext-only Attack

In a ciphertext-only attack, the attacker only has access to the encrypted message (ciphertext). The goal is to deduce the plaintext or the key, solely from analyzing the encrypted message. This is by far the most challenging of the attacks. A ciphertext-only attack requires a deep understanding of the structure and weaknesses of the encryption algorithm. Attackers may use statistical analysis, look for patterns corresponding to probable plaintext structures, or employ brute force methods to try a wide range of possible keys. This method is often seen in scenarios where an interceptor can only access communication channels to collect encrypted messages. This attack is popular in movies but not in real life.

Example: If an attacker intercepts encrypted communications (ciphertext) but has no knowledge of the plaintext or the encryption key, they must analyze the ciphertext, searching for statistical abnormalities or patterns in the ciphertext to make inferences. In simpler ciphers, like the Caesar cipher, letter frequency analysis could be used if the ciphertext is long enough.

Bits are bits

In all these cases, attackers must have an idea of what they’re looking for – what the decrypted text can represent. Bits are bits - they’re ones and zeroes, and decrypting anything, correctly or not, produces a different set of ones and zeroes. An attacker will have to test decrypted results to determine if they ave a successful decryption. For example, they might know they’re looking for zip or jpeg data and will check for appropriate headers; or they might suspect the decrypted content would be French text and can check for the right statistical distribution of characters, set of characters, or expected strings.

Industry-standard modern ciphers are secure against techniques such as frequency analysis and searching for coincidences (repetitions). They don’t have discoverable anomalies that result in any detectable statistical correlations between the plaintext and ciphertext or between the key and ciphertext.

Linear cryptanalysis

Linear cryptanalysis is a technique used to attack block ciphers. This approach tries to formulate linear equations that approximate the non-linear relationship between the plaintext, ciphertext, and key in the actual cipher. The goal is not to replicate the cipher (which is not possible) but to uncover any correlations within the bit patterns that could suggest a more targeted approach to finding the key. These correlations, while not providing a direct solution, offer a significant lever in reducing the complexity of the cryptanalyst’s task.

Cryptanalysts look for correlations between the plaintext, ciphertext, and key bits, attempting to exploit any biases in these correlations to provide information about some bits of the key.

How it works: Attackers form linear equations relating the plaintext, key, and ciphertext, and then, using many known plaintext-ciphertext pairs, they test which key bits satisfy these equations most often (i.e., statistically more than random). Linear cryptanalysis usually targets only one or a few bits at a time, trying to find a linear relation between some parts of the plaintext, some part of the key, and some parts of the resulting ciphertext.

Example: Linear cryptanalysis was first successfully applied to the DES (Data Encryption Standard) cipher. By analyzing many plaintext-ciphertext pairs, cryptanalysts could approximate the behavior of the S-boxes (non-linear components in DES) and recover the key with significantly less work than brute force.

Differential cryptanalysis

Differential cryptanalysis is an approach where analysts study the effects of specific alterations in plaintext on the resulting ciphertext. By analyzing how these changes propagate through the encryption process, cryptanalysts can detect patterns or inconsistencies that certain keys may introduce. This method does not rely on chance; it is an exercise in pattern recognition and statistical analysis, seeking to understand the inner workings of the cipher.

How it works: The attacker examines pairs of plaintexts with specific differences and observes how these differences propagate through the rounds of the cipher. By comparing the resulting ciphertexts, they can deduce how certain key bits influence these differences.

Example: Differential cryptanalysis was also applied to DES. In this attack, pairs of plaintexts differing by a fixed amount (called a “difference”) were encrypted, and the attacker studied the difference in the corresponding ciphertexts. By doing this over many pairs, cryptanalysts could eventually recover the secret key.

Neither differential nor linear cryptanalysis promises immediate decryption. Instead, they are tools that refine the search for the cryptographic key, narrowing down the vast field of possibilities to a — hopefully — more manageable scope. This refinement process is similar to filtering noise from a signal, allowing cryptanalysts to focus their computational resources on the most promising areas. Both of these techniques rely on large volumes of plaintext data and its corresponding ciphertext to perform the analysis.

As encryption technologies continue to evolve, so too does the field of cryptanalysis. It remains an arms race between encryption designers and cryptanalysts, with each advancement in cryptographic techniques met with an equally innovative approach to cryptanalysis. The work is meticulous, methodical, and requires a deep understanding of both the mathematics underpinning cryptography and the practical applications of these mathematical principles.

References

Fred Cohen, 2.1 - A Short History of Cryptography, 1995.

Alberti Cipher Disk, Wikipedia.

Daniel Rodriguez-Clark, Caesar Shift Cipher, Crypto Corner, 2019. - **includes interactive examples **

Simon Singh, Cracking the Vigenère Cipher, The Black Chamber, 2000. Daniel Rodriguez-Clark, Vigenère Cipher, Crypto Corner, 2019. - **includes interactive examples **

One-time Pad

Wikipedia, One-time Pad

Data Encryption Standard, Wikipedia.

Sanchita Mal-Sarkar and Chansu Yu, Data Encryption Standard, Hands-on Experience on Computer System Security.

Advanced Encryption Standard process, Wikipedia.

Josh Lake, What is AES Encryption and how does it work?, Comparitech, 2020.