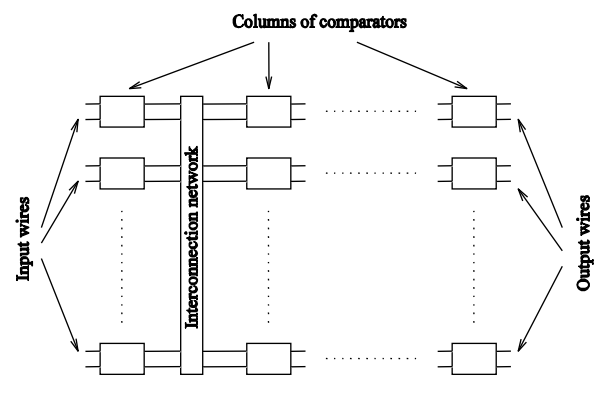
An example of a bitonic sorting network. Diagram from
Bitonic sort is a comparison-based sorting algorithm that can be run in
parallel.
It focuses on converting a random sequence of numbers into a
bitonic sequence, one that monotonically increases, then
decreases.
Rotations of a bitonic sequence are also bitonic.
More specifically, bitonic sort can be modelled as a type of sorting
network.
The initial unsorted sequence enters through input pipes,
where a series of comparators switch two entries to be in either
increasing or decreasing order.
The algorithm, created by Ken Batcher in 1968, consists of two parts. First, the unsorted sequence is built into a bitonic sequence; then, the series is split multiple times into smaller sequences until the input is in sorted order.

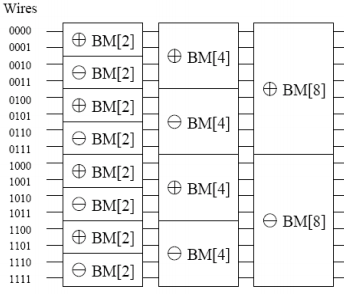
The bitonic split is a procedure that cuts one bitonic sequence into two smaller ones, where all the elements of the first sequence are less than or equal to the ones in the second. Looking at the example below, a bitonic sequence is divided between its two halves, and the n th element in each part is compared with each other. If they are out of order, they are swapped. Applying this procedure repeatedly onto the smaller lists, the result is a sorted sequence in ascending order.

Before the sorting can occur, the original sequence must first be transformed into a bitonic one. Note that two numbers by themselves are a bitonic sequence; from that, the sequence can be partitioned into smaller bitonic ones and then merged together.
The building algorithm is a variation of the bitonic split: two adjacent bitonic sequences are split and sorted in ascending order, the next two in descending order, and so on. The orinial two sequences are now a single bitonic sequence. This procedure continues until the entirety of the input has been converted.
Here is an example of the build algorithm applied to a list of integers:

This code, written in C, applies bitonic sort to a list of integers given in a text file.
When run in serial, the bitonic sorting network completes its work in O(n log2n) comparisons, which falls short of the ideal comparison-based sort efficiency of O(n log n). Parallel versions of the sort, however, can lead to dramatic speedups, depending on the implementation.