Trains
Vending
Minesweeper
The figure below shows a simple train network.
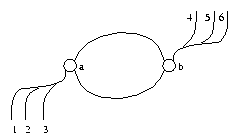
A single engine, which we can refer to as e, travels back and forth from station a to station b. At station a there are three ports, p1, p2, and p3, where the train can pick up or discharge cars. There are another three ports, p4, p5, and p6, at station b.
Informally, there are three kinds of actions available in this train domain. The first part of this problem is to formalize these actions in the STRIPS action representation -- indicating what the preconditions of each action are, what relationships the action disrups (which go on a delete list for the action), and what relationships the action establishes (which go on an add list for the action). The actions are:
- Going to a station. Possible only if the train is already at the other station, this action ends the relationship of the train being at the current station and establishes that the train is at the new destination.
- Hooking up a given car from a given port. This action is possible only if that car is currently stationed at that port, and if the engine is currently waiting at the station to which that port leads. As a result, the car is no longer stationed at the port - the port is now empty - and instead the car is located at the end of the train following whatever car was on the end of the train earlier.
- Unhooking a given car onto a given port. This action is possible only if the car is the last one on the train, the train is currently waiting at the station to which the destination port leads, and the destination port is currently empty. The result of the action is that the last car on the train goes into the port (and the port is therefore filled), while the previous car on the train becomes the new last car.
Consider the following situation. The engine, with no cars attached, is located at station a. All of the ports are empty, except p4, which contains car c1 which is loaded with a tank of orange juice. We want to get c1 into port p1 where the orange juice can be bottled and distributed to local stores.
- Represent the unchanging facts that characterize the train network and that your formalization of action preconditions requires in order to classify actions as possible or impossible in this situation or situations that could evolve from it.
- Represent the initial situation for this planning problem.
- Spell out a sequence of actions that will achieve the desired goal.
- Indicate the successive states resulting from each step in the execution of this plan.
Now we consider a more complicated situation. We still want to get the tank of orange juice from p4 to p1, but now things start off like this. The engine is at station b, and, as before, car c1 is at p4 and ports p5 and p6 are empty. However, there is a car at each of the ports at station a: p1 has c2 p2 has c3 and p3 has c4.
- Spell out a sequence of actions that will achieve the desired goal in this situation. In addition, make sure that this plan leaves all the cars associated with the same stations where they started out. (Use as few unhooks as you can.)
- Suppose instead that c3 didn't exist so that p2 starts out empty. Spell out a plan with fewer actions to achieve the goal in this situation.
- Both plans must achieve the goal by eventually unhooking car c1 onto port p1. Call this action u. Indicate the causal links in the two plans that are associated with the preconditions of u.
- Describe how the differences in causal links affects the threats that arise in coming up with the two plans; in particular, what effect does the difference in causal links have on the order of actions and the number of actions in the plan?
Many campus buildings at Rutgers are stocked with a certain kind of vending machine that dispenses candy and other snacks. You put some money in it, and then enter two digits that indicate what your selection was. A screw at the coordinates you've specified turns to release the food you have selected, while at the same time any change for your purchase is rung out for you.
This problem looks at formalizing and analyzing a simplified version of this behavior, using the situation calculus. Our first idealization is a generous one - we abstract away from the fact that this machine actually requires money to operate and just assume that it gives out candy whenever you make a selection into it. The second idealization is to narrow down the buttons to a single set of four buttons that you can use to specify both coordinates of a selection. These buttons will be called a, b, c and d - and we can use these to go proxy for the actions of pressing these buttons.
-
Here is a situation calculus axiom that at first glance seems
like it describes the behavior of this machine in dispensing
starbursts when you select bd:
dispensed(starburst,do(d,do(b,S))).
What's wrong with this axiom?
- We can explicitly use a predicate that describes the state of the machine to formalize the machine better. Let's have five states: wait for when no buttons have been pressed and sa through sd for the different states when the first coordinate of a selection has been entered but the second has not. Break up the above axiom into two to account for the actual behavior of the machine in dispensing starbursts.
-
Suppose you walk up to the machine and press d (hoping
to get a snickers, from da) but immediately the machine
gives you a starburst. In other words, you observe:
dispensed(starburst,do(d,S))
Give two formal explanations for this observation based on assumptions about the state of the machine. How are these two explanations related?
Minesweeper is a common single-player computer game. It's played on a grid; cells on the grid are initially concealed and may be explored by clicking on them. Some of the cells hide bombs; clicking on them loses you the game. Fortunately, when you explore a cell with no bombs - a clear cell - you learn information about the cells nearby. Each exposed clear cell gets labeled with the number of bombs located in the adjacent cells (e.g., the eight neighboring cells for a cell in the middle of the board).
For example, we can use @ to represent a bomb and ^ to represent a clear cell; suppose the grid actually contains clear cells and bombs as follows:
| @ | ^ | @ |
| ^ | ^ | ^ |
| ^ | @ | ^ |
Then clicking on the center square will reveal the number three, indicating that three of the eight adjacent squares actually contain bombs.
Here is a more complicated board, with ?'s in the unexplored cells to give you the view of the board as a minesweeper player might actually see it:
| ? | ? | ? | 0 |
| ? | ? | 2 | 0 |
| ? | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 |
(Treat the board as complete, so that tallies for cells on the boundary only report the three or five adjacent cells that are represented in the board diagram.)
You can formulate a constraint satisfaction problem to figure out where there must be bombs (and where there may or may not be bombs) according to these counts.
- Write down the variables of the constraint satisfaction problem (and indicate what each of these variables is intended to represent).
- Write down the domains (or set of candidate values) for each of these variables.
- Write down the constraints on the values of the variables as a set of mathematical or logical expressions.
- Draw a constraint network diagram indicating the dependencies among the variables in the problem; use an extended arc-consistency method to refine the domains until they are domain-consistent and arc-consistent. In the final version that you get what values are associated with each variable?
- If any variables are associated with multiple values, describe what these multiple values say about the constraint satisfaction problem corresponding to this minesweeper board.
Here is a board that looks simpler but requires more complicated reasoning than the board we just treated.
| ? | 1 |
| ? | 1 |
| ? | 1 |
| ? | 1 |
- Answer the same five questions for this board.
- Take any of the variables you used, and assign it a definite value; then perform arc consistency again. What happens? Try setting it to another value and performing arc-consistency. What happens now?
- What does this say about constraint-satisfaction search?