Non-parametric Background Subtraction
Ahmed Elgammal - David Harwood - Larry Davis
Computer Vision Laboratory
University of Maryland,
College Park, MD, 20742, USA
1 Introduction
The detection of unusual motion is
the first stage in many automated visual surveillance applications. It is
always desirable to achieve very high sensitivity in the detection of moving
objects with the lowest possible false alarm rates. Background subtraction is a
method typically used to detect unusual motion in the scene by comparing each
new frame to a model of the scene background.
In many visual surveillance
applications that work with outdoor scenes, the background of the scene
contains many non-static objects such as tree branches and bushes whose
movement depends on the wind in the scene. This kind of background motion
causes the pixel intensity values to vary significantly with time. For example,
one pixel can be image of the sky at one frame, tree leaf at another frame,
tree branch on a third frame and some mixture subsequently; in each situation
the pixel will have a different color.
We present a nonparametric technique for modeling the background of scene. The approach is based on kernel density estimation of the probability density function of the intensity of each pixel given a sample for this pixel.
2.1 Density Estimation
The objective of the model is to capture very recent information about the image sequence, continuously updating this information to capture fast changes in the scene background. The intensity distribution of a pixel can change quickly. So we must estimate the density function of this distribution at any moment of time given only very recent history information if we hope to obtain sensitive detection.
Let x1,…,xN be a recent sample of intensity values for a pixel. Using this sample, the probability density function that this pixel will have intensity value xt at time t can be non-parametrically estimated using the kernel Kh as
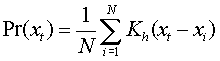
If we choose our kernel estimator function, Kh, to be a Gaussian kernel , Kh = N(0,S) where S represents the kernel function bandwidth, and we assume diagonal correlation matrix S with a different kernel bandwidths sj for the jth color channel, then the density can be estimated as
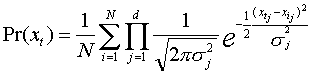
Using this probability estimate the, pixel is considered a foreground pixel if Pr(xt) < th , where the threshold th is a global threshold over all the image that can be adjusted to achieve a desired percentage of false positives. Practically, the probability estimation can be calculated in a very fast way using pre calculated lookup tables for the kernel function values given the intensity value difference, (xt - xi) , and the kernel function bandwidth. Moreover, a partial evaluation of the summation is usually sufficient to surpass the threshold at most image pixels, since most of the image is typically sampled from the background. This allows a very fast implementation of the probability estimation.
|
|
|
|
|
( a ) |
( b ) |
( c ) |
2.2 Kernel Width Estimation
There are at least two sources of variations in a pixel's intensity value. First, there are large jumps between different intensity values because different objects (sky, branch, leaf and mixtures when an edge passes through the pixel) are projected to the same pixel at different times. Second, for those very short periods of time when the pixel is a projection of the same object, there is local intensity variation due to blurring in the image. The kernel bandwidth, s2, should reflect the local variance in the pixel intensity due to the local variation from image blur and not the intensity jumps. This local variance will vary over the image and change over time. The local variance is also different among the color channels, requiring different bandwidth for each color channel in the kernel calculation.
To estimate the kernel bandwidth, sj2, for the jth color channel for a given pixel we compute the median absolute deviation over the sample for consecutive intensity values of the pixel. That is, the median, m, of | xi – xi+1 | for each consecutive pair ( xi , xi+1 ) in the sample, is calculated independently for each color channel. Since we are measuring deviations between two consecutive intensity values, the pair ( xi , xi+1 ) usually comes from the same local-in-time distribution and only few pairs are expected to come from cross distributions. If we assume that this local-in-time distribution is Normal N(m,s2), then the deviation (xi – xi+1 ) is Normal N(0,2s2). So the standard deviation of the first distribution can be estimated as:
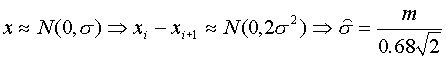
Since the deviations are integer values, linear interpolation is used to obtain more accurate median values.
3 Probabilistic Suppression of False Detection
In outdoor environments with fluctuating backgrounds, there are two sources of false detections. First, there are false detections due to random noise that should be homogeneous over the entire image. Second, there are false detections due to small movements in the scene background that are not represented in the background model. This can occur, for example, if a tree branch moves further than it did during model generation. Also small camera displacements due to wind load are common in outdoor surveillance and cause many false detection.
The second stage of detection aims to suppress the false detections due to small and un-modeled movements in the scene background. If some part of the background (a tree branch for example) moves to occupy a new pixel, but it was not part of the model for that pixel, then it will be detected as a foreground object. However, this object will have a high probability to be a part of the background distribution at its original pixel. Assuming that only a small displacement can occur between consecutive frames, we decide if a background object motion has caused a false detection by considering the background distributions in a small neighborhood of the detection.
Let xt be the observed value of a pixel, x, detected as a foreground pixel by the first stage of the background subtraction at time t. We define the pixel displacement probability, Rw(xt) , to be the maximum probability that the observed value, xt , belongs to the background distribution of some point in the neighborhood w(x)
![]()
where By is the background sample for pixel y and the probability estimation, Pr(xt | By) , is calculated using the kernel function estimation as in section 2. By thresholding Rw for detected pixels we can eliminate many false detections due to small motions in the background. We add the constraint that the whole detected foreground object must have moved from a nearby location, and not only some of its pixels. We define the component displacement probability, PC , to be the probability that a detected connected component has been displaced from a nearby location. This probability is estimated by
![]()
For a connected component corresponding to a real target,
the probability that this component has displaced from the background will be
very small. So, a detected pixel, x, will be considered to be a part of the
background only if ![]() .
.
|
|
||
|
( a ) |
( b ) |
( c ) |
|
Figure 2: Probabilistic suppression false detections. (a) Original image. (b) Background subtraction result. Note the clustered false detection around the edges. (c) Result after probabilistic false positive suppression. |
||
Figure 2 illustrates the effect of false detection suppression. As a result of the wind load, the outdoor camera is shaking slightly which results in a lot of clustered false detections especially on the edges (figure 2b). After evaluating component displacement probabilities, most of these clustered false detections are suppressed while the small target at the left side of the image remains (figure 2c).
4 Updating The Background
In the
previous sections it was shown how to detect foreground regions given a recent
history sample as a model of the background. This sample contains N
intensity values taken over a window in time of size W. The kernel
bandwidth estimation requires all the sample to be consecutive in time, i.e., N=W
or sample N/2 pairs of consecutive intensity values over time W.
This sample needs to be updated continuously to adapt to changes in the scene.
The update is performed in a first-in first-out manner. That is, the oldest
sample/pair is discarded and a new sample/pair is added to the model. The new
sample is chosen randomly from each interval of length W/N frames.
There are tradeoffs corresponding to the update decision regarding how fast to
update and where to update in the image. We studied the use of two different
background models (short term and long term models) to overcome some of these
tradoffs. The details can be found in [1]
|
Some examples video
clips. More examples
can be found at: ftp://www.umiacs.umd.edu/pub/elgammal/video/index.html |
||
Publication:
1 - Ahmed Elgammal, David Harwood, Larry Davis “Non-parametric Model for Background Subtraction” 6th European Conference on Computer Vision. Dublin, Ireland, June/July 2000. [PDF]






